2D Plots
Drawing 2D figures
In this lecture, we will make 2D figures
import numpy as np
import matplotlib.pyplot as plt
from netCDF4 import Dataset, num2date
import matplotlib
# %matplotlib qt
# Figures in a separate window
# %matplotlib inline # Figures in this browser
Read the temperature data
We are going to read two datasets: one for the mean temperature (absolute.nc) and the other one for the time series of temperature anomaly (HadCRUT.4.6.0.0.median.nc).
f = Dataset('absolute.nc', 'r')
print(f.variables.keys())
T = f.variables['tem'][:] # monthly data
lon = f.variables['lon'][:]
lat = f.variables['lat'][:]
f.close()
odict_keys(['tem', 'lat', 'lon', 'time'])
f = Dataset('HadCRUT.4.6.0.0.median.nc', 'r')
print(f.variables.keys())
Tanom = f.variables['temperature_anomaly'][:]
time = f.variables['time'][:]
lon = f.variables['longitude'][:]
lat = f.variables['latitude'][:]
# print(f.variables['time'])
f.close()
odict_keys(['latitude', 'longitude', 'time', 'temperature_anomaly', 'field_status'])
The size of Tanom is
T.shape
(12, 36, 72)
Plot temperature 2D plot
Let’s make a plot of T in 1850
T1850 = T[0, :, :] + Tanom[0, :, :] # This is the monthly mean
imshow
The simplest way to visualize a 2D variable is imshow. This function gives colors to each element of the array without considering grid information. It is fast and a good tool to check the variable.
help(plt.imshow)
Help on function imshow in module matplotlib.pyplot:
imshow(X, cmap=None, norm=None, aspect=None, interpolation=None, alpha=None, vmin=None, vmax=None, origin=None, extent=None, shape=None, filternorm=1, filterrad=4.0, imlim=None, resample=None, url=None, *, data=None, **kwargs)
Display an image, i.e. data on a 2D regular raster.
Parameters
----------
X : array-like or PIL image
The image data. Supported array shapes are:
- (M, N): an image with scalar data. The data is visualized
using a colormap.
- (M, N, 3): an image with RGB values (float or uint8).
- (M, N, 4): an image with RGBA values (float or uint8), i.e.
including transparency.
The first two dimensions (M, N) define the rows and columns of
the image.
The RGB(A) values should be in the range [0 .. 1] for floats or
[0 .. 255] for integers. Out-of-range values will be clipped to
these bounds.
cmap : str or `~matplotlib.colors.Colormap`, optional
A Colormap instance or registered colormap name. The colormap
maps scalar data to colors. It is ignored for RGB(A) data.
Defaults to :rc:`image.cmap`.
aspect : {'equal', 'auto'} or float, optional
Controls the aspect ratio of the axes. The aspect is of particular
relevance for images since it may distort the image, i.e. pixel
will not be square.
This parameter is a shortcut for explicitly calling
`.Axes.set_aspect`. See there for further details.
- 'equal': Ensures an aspect ratio of 1. Pixels will be square
(unless pixel sizes are explicitly made non-square in data
coordinates using *extent*).
- 'auto': The axes is kept fixed and the aspect is adjusted so
that the data fit in the axes. In general, this will result in
non-square pixels.
If not given, use :rc:`image.aspect` (default: 'equal').
interpolation : str, optional
The interpolation method used. If *None*
:rc:`image.interpolation` is used, which defaults to 'nearest'.
Supported values are 'none', 'nearest', 'bilinear', 'bicubic',
'spline16', 'spline36', 'hanning', 'hamming', 'hermite', 'kaiser',
'quadric', 'catrom', 'gaussian', 'bessel', 'mitchell', 'sinc',
'lanczos'.
If *interpolation* is 'none', then no interpolation is performed
on the Agg, ps and pdf backends. Other backends will fall back to
'nearest'.
See
:doc:`/gallery/images_contours_and_fields/interpolation_methods`
for an overview of the supported interpolation methods.
Some interpolation methods require an additional radius parameter,
which can be set by *filterrad*. Additionally, the antigrain image
resize filter is controlled by the parameter *filternorm*.
norm : `~matplotlib.colors.Normalize`, optional
If scalar data are used, the Normalize instance scales the
data values to the canonical colormap range [0,1] for mapping
to colors. By default, the data range is mapped to the
colorbar range using linear scaling. This parameter is ignored for
RGB(A) data.
vmin, vmax : scalar, optional
When using scalar data and no explicit *norm*, *vmin* and *vmax*
define the data range that the colormap covers. By default,
the colormap covers the complete value range of the supplied
data. *vmin*, *vmax* are ignored if the *norm* parameter is used.
alpha : scalar, optional
The alpha blending value, between 0 (transparent) and 1 (opaque).
This parameter is ignored for RGBA input data.
origin : {'upper', 'lower'}, optional
Place the [0,0] index of the array in the upper left or lower left
corner of the axes. The convention 'upper' is typically used for
matrices and images.
If not given, :rc:`image.origin` is used, defaulting to 'upper'.
Note that the vertical axes points upward for 'lower'
but downward for 'upper'.
extent : scalars (left, right, bottom, top), optional
The bounding box in data coordinates that the image will fill.
The image is stretched individually along x and y to fill the box.
The default extent is determined by the following conditions.
Pixels have unit size in data coordinates. Their centers are on
integer coordinates, and their center coordinates range from 0 to
columns-1 horizontally and from 0 to rows-1 vertically.
Note that the direction of the vertical axis and thus the default
values for top and bottom depend on *origin*:
- For ``origin == 'upper'`` the default is
``(-0.5, numcols-0.5, numrows-0.5, -0.5)``.
- For ``origin == 'lower'`` the default is
``(-0.5, numcols-0.5, -0.5, numrows-0.5)``.
See the example :doc:`/tutorials/intermediate/imshow_extent` for a
more detailed description.
shape : scalars (columns, rows), optional, default: None
For raw buffer images.
filternorm : bool, optional, default: True
A parameter for the antigrain image resize filter (see the
antigrain documentation). If *filternorm* is set, the filter
normalizes integer values and corrects the rounding errors. It
doesn't do anything with the source floating point values, it
corrects only integers according to the rule of 1.0 which means
that any sum of pixel weights must be equal to 1.0. So, the
filter function must produce a graph of the proper shape.
filterrad : float > 0, optional, default: 4.0
The filter radius for filters that have a radius parameter, i.e.
when interpolation is one of: 'sinc', 'lanczos' or 'blackman'.
resample : bool, optional
When *True*, use a full resampling method. When *False*, only
resample when the output image is larger than the input image.
url : str, optional
Set the url of the created `.AxesImage`. See `.Artist.set_url`.
Returns
-------
image : `~matplotlib.image.AxesImage`
Other Parameters
----------------
**kwargs : `~matplotlib.artist.Artist` properties
These parameters are passed on to the constructor of the
`.AxesImage` artist.
See also
--------
matshow : Plot a matrix or an array as an image.
Notes
-----
Unless *extent* is used, pixel centers will be located at integer
coordinates. In other words: the origin will coincide with the center
of pixel (0, 0).
There are two common representations for RGB images with an alpha
channel:
- Straight (unassociated) alpha: R, G, and B channels represent the
color of the pixel, disregarding its opacity.
- Premultiplied (associated) alpha: R, G, and B channels represent
the color of the pixel, adjusted for its opacity by multiplication.
`~matplotlib.pyplot.imshow` expects RGB images adopting the straight
(unassociated) alpha representation.
.. note::
In addition to the above described arguments, this function can take a
**data** keyword argument. If such a **data** argument is given, the
following arguments are replaced by **data[<arg>]**:
* All positional and all keyword arguments.
Objects passed as **data** must support item access (``data[<arg>]``) and
membership test (``<arg> in data``).
As shown above, you do not pass grid information to imshow.
T1850
masked_array(
data=[[--, --, --, ..., --, --, --],
[--, --, --, ..., --, --, --],
[--, --, --, ..., --, --, --],
...,
[--, --, --, ..., --, --, --],
[--, --, --, ..., --, --, --],
[--, --, --, ..., --, --, --]],
mask=[[ True, True, True, ..., True, True, True],
[ True, True, True, ..., True, True, True],
[ True, True, True, ..., True, True, True],
...,
[ True, True, True, ..., True, True, True],
[ True, True, True, ..., True, True, True],
[ True, True, True, ..., True, True, True]],
fill_value=1e+20)
f, ax = plt.subplots(1, 1, figsize=(12, 5))
c = ax.imshow(T1850)
plt.colorbar(c)
<matplotlib.colorbar.Colorbar at 0x11bb3cb38>
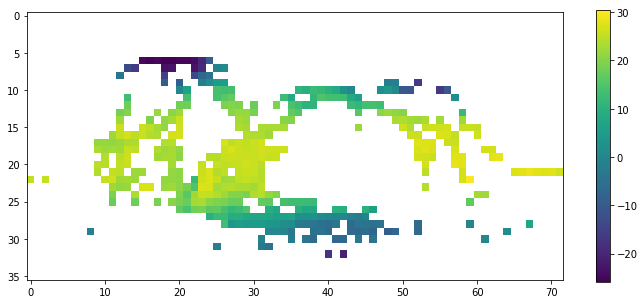
imshow askes for a special argument if you want to modify the aspect ratio.
f, ax = plt.subplots(1, 1, figsize=(15, 15))
c = ax.imshow(T1850, aspect='auto')
plt.colorbar(c)
<matplotlib.colorbar.Colorbar at 0x112cad470>
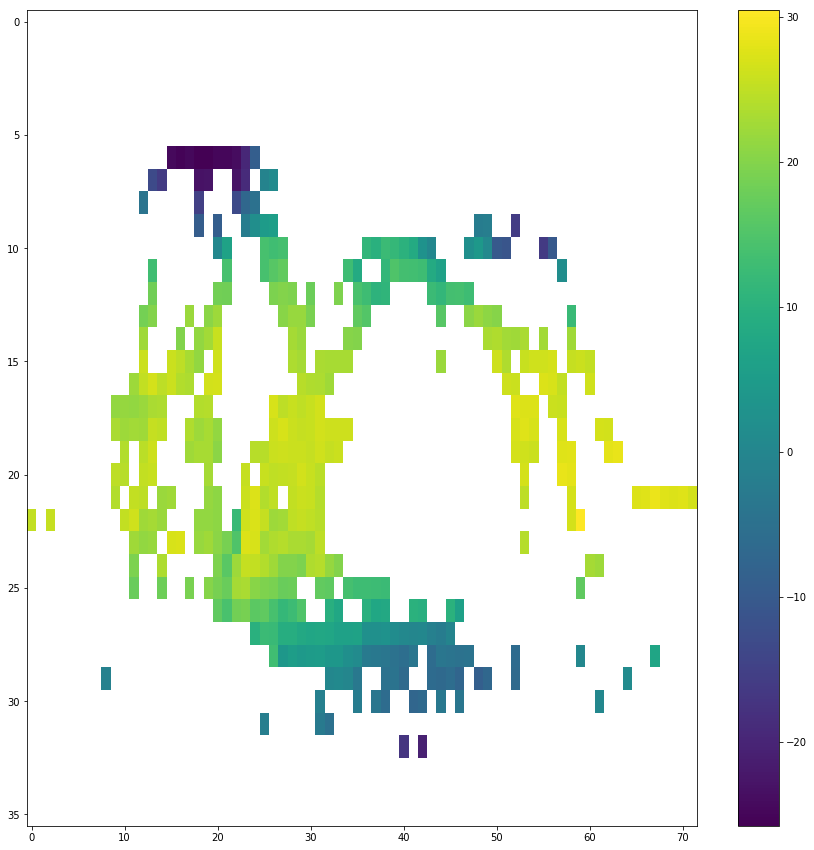
You can twick the figure with different colormap, origin, interpolation, vmin and vmax.
f, ax = plt.subplots(2, 2, figsize=(15, 8))
ax[0,0].imshow(T1850, origin='lower')
ax[0,1].imshow(T1850, cmap='rainbow') # more at https://matplotlib.org/examples/color/colormaps_reference.html
ax[1,0].imshow(T1850, interpolation='bilinear')
ax[1,1].imshow(T1850, vmin=0, vmax=30)
<matplotlib.image.AxesImage at 0x11ba4fd30>
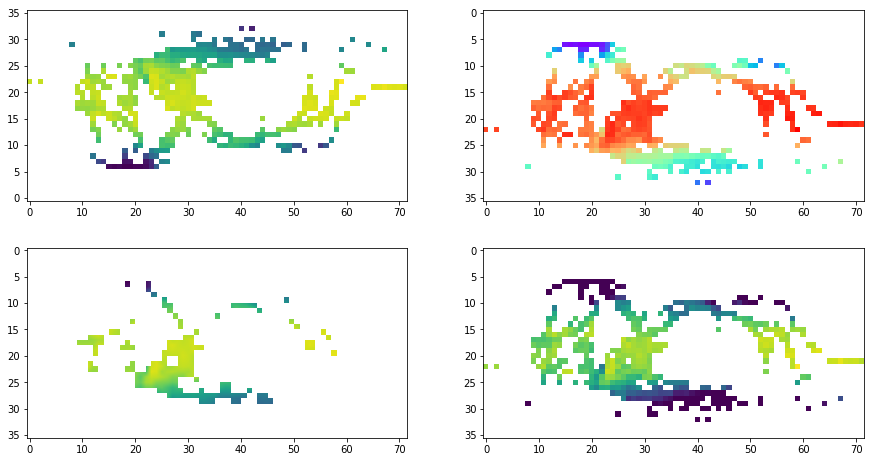
pcolormesh
You can use pcolormesh in the same manner as imshow, but you can also pass the grid information.
help(plt.pcolormesh)
Help on function pcolormesh in module matplotlib.pyplot:
pcolormesh(*args, alpha=None, norm=None, cmap=None, vmin=None, vmax=None, shading='flat', antialiased=False, data=None, **kwargs)
Create a pseudocolor plot with a non-regular rectangular grid.
Call signature::
pcolor([X, Y,] C, **kwargs)
*X* and *Y* can be used to specify the corners of the quadrilaterals.
.. note::
``pcolormesh()`` is similar to :func:`~Axes.pcolor`. It's much
faster and preferred in most cases. For a detailed discussion on
the differences see
:ref:`Differences between pcolor() and pcolormesh()
<differences-pcolor-pcolormesh>`.
Parameters
----------
C : array_like
A scalar 2-D array. The values will be color-mapped.
X, Y : array_like, optional
The coordinates of the quadrilateral corners. The quadrilateral
for ``C[i,j]`` has corners at::
(X[i+1, j], Y[i+1, j]) (X[i+1, j+1], Y[i+1, j+1])
+--------+
| C[i,j] |
+--------+
(X[i, j], Y[i, j]) (X[i, j+1], Y[i, j+1]),
Note that the column index corresponds to the
x-coordinate, and the row index corresponds to y. For
details, see the :ref:`Notes <axes-pcolormesh-grid-orientation>`
section below.
The dimensions of *X* and *Y* should be one greater than those of
*C*. Alternatively, *X*, *Y* and *C* may have equal dimensions, in
which case the last row and column of *C* will be ignored.
If *X* and/or *Y* are 1-D arrays or column vectors they will be
expanded as needed into the appropriate 2-D arrays, making a
rectangular grid.
cmap : str or `~matplotlib.colors.Colormap`, optional
A Colormap instance or registered colormap name. The colormap
maps the *C* values to colors. Defaults to :rc:`image.cmap`.
norm : `~matplotlib.colors.Normalize`, optional
The Normalize instance scales the data values to the canonical
colormap range [0, 1] for mapping to colors. By default, the data
range is mapped to the colorbar range using linear scaling.
vmin, vmax : scalar, optional, default: None
The colorbar range. If *None*, suitable min/max values are
automatically chosen by the `~.Normalize` instance (defaults to
the respective min/max values of *C* in case of the default linear
scaling).
edgecolors : {'none', None, 'face', color, color sequence}, optional
The color of the edges. Defaults to 'none'. Possible values:
- 'none' or '': No edge.
- *None*: :rc:`patch.edgecolor` will be used. Note that currently
:rc:`patch.force_edgecolor` has to be True for this to work.
- 'face': Use the adjacent face color.
- An mpl color or sequence of colors will set the edge color.
The singular form *edgecolor* works as an alias.
alpha : scalar, optional, default: None
The alpha blending value, between 0 (transparent) and 1 (opaque).
shading : {'flat', 'gouraud'}, optional
The fill style, Possible values:
- 'flat': A solid color is used for each quad. The color of the
quad (i, j), (i+1, j), (i, j+1), (i+1, j+1) is given by
``C[i,j]``.
- 'gouraud': Each quad will be Gouraud shaded: The color of the
corners (i', j') are given by ``C[i',j']``. The color values of
the area in between is interpolated from the corner values.
When Gouraud shading is used, *edgecolors* is ignored.
snap : bool, optional, default: False
Whether to snap the mesh to pixel boundaries.
Returns
-------
mesh : `matplotlib.collections.QuadMesh`
Other Parameters
----------------
**kwargs
Additionally, the following arguments are allowed. They are passed
along to the `~matplotlib.collections.QuadMesh` constructor:
agg_filter: a filter function, which takes a (m, n, 3) float array and a dpi value, and returns a (m, n, 3) array
alpha: float or None
animated: bool
antialiased: bool or sequence of bools
array: ndarray
capstyle: {'butt', 'round', 'projecting'}
clim: a length 2 sequence of floats; may be overridden in methods that have ``vmin`` and ``vmax`` kwargs.
clip_box: `.Bbox`
clip_on: bool
clip_path: [(`~matplotlib.path.Path`, `.Transform`) | `.Patch` | None]
cmap: colormap or registered colormap name
color: matplotlib color arg or sequence of rgba tuples
contains: callable
edgecolor: color or sequence of colors
facecolor: color or sequence of colors
figure: `.Figure`
gid: str
hatch: {'/', '\\', '|', '-', '+', 'x', 'o', 'O', '.', '*'}
in_layout: bool
joinstyle: {'miter', 'round', 'bevel'}
label: object
linestyle: {'-', '--', '-.', ':', '', (offset, on-off-seq), ...}
linewidth: float or sequence of floats
norm: `.Normalize`
offset_position: {'screen', 'data'}
offsets: float or sequence of floats
path_effects: `.AbstractPathEffect`
picker: None or bool or float or callable
pickradius: unknown
rasterized: bool or None
sketch_params: (scale: float, length: float, randomness: float)
snap: bool or None
transform: `.Transform`
url: str
urls: List[str] or None
visible: bool
zorder: float
See Also
--------
pcolor : An alternative implementation with slightly different
features. For a detailed discussion on the differences see
:ref:`Differences between pcolor() and pcolormesh()
<differences-pcolor-pcolormesh>`.
imshow : If *X* and *Y* are each equidistant, `~.Axes.imshow` can be a
faster alternative.
Notes
-----
**Masked arrays**
*C* may be a masked array. If ``C[i, j]`` is masked, the corresponding
quadrilateral will be transparent. Masking of *X* and *Y* is not
supported. Use `~.Axes.pcolor` if you need this functionality.
.. _axes-pcolormesh-grid-orientation:
**Grid orientation**
The grid orientation follows the standard matrix convention: An array
*C* with shape (nrows, ncolumns) is plotted with the column number as
*X* and the row number as *Y*.
.. _differences-pcolor-pcolormesh:
**Differences between pcolor() and pcolormesh()**
Both methods are used to create a pseudocolor plot of a 2-D array
using quadrilaterals.
The main difference lies in the created object and internal data
handling:
While `~.Axes.pcolor` returns a `.PolyCollection`, `~.Axes.pcolormesh`
returns a `.QuadMesh`. The latter is more specialized for the given
purpose and thus is faster. It should almost always be preferred.
There is also a slight difference in the handling of masked arrays.
Both `~.Axes.pcolor` and `~.Axes.pcolormesh` support masked arrays
for *C*. However, only `~.Axes.pcolor` supports masked arrays for *X*
and *Y*. The reason lies in the internal handling of the masked values.
`~.Axes.pcolor` leaves out the respective polygons from the
PolyCollection. `~.Axes.pcolormesh` sets the facecolor of the masked
elements to transparent. You can see the difference when using
edgecolors. While all edges are drawn irrespective of masking in a
QuadMesh, the edge between two adjacent masked quadrilaterals in
`~.Axes.pcolor` is not drawn as the corresponding polygons do not
exist in the PolyCollection.
Another difference is the support of Gouraud shading in
`~.Axes.pcolormesh`, which is not available with `~.Axes.pcolor`.
.. note::
In addition to the above described arguments, this function can take a
**data** keyword argument. If such a **data** argument is given, the
following arguments are replaced by **data[<arg>]**:
* All positional and all keyword arguments.
Objects passed as **data** must support item access (``data[<arg>]``) and
membership test (``<arg> in data``).
# Use pcolormesh as imshow
f, ax = plt.subplots(1, 1, figsize=(12, 5))
c = ax.pcolormesh(T1850)
plt.colorbar(c)
<matplotlib.colorbar.Colorbar at 0x11fb12630>
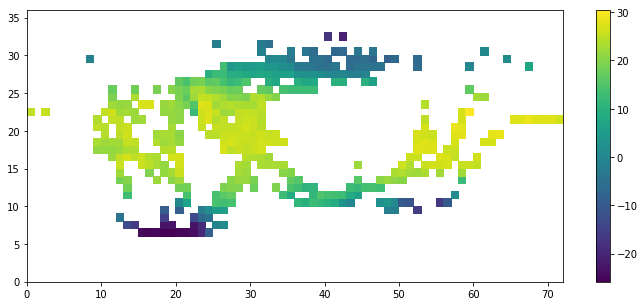
f, ax = plt.subplots(1, 2, figsize=(12, 5))
ax[0].imshow(T1850[20:25, 20:30])
ax[0].grid('on')
ax[1].pcolormesh(T1850[20:25, 20:30])
ax[1].grid('on')
/Users/hajsong/miniconda2/envs/py36/lib/python3.6/site-packages/matplotlib/cbook/__init__.py:424: MatplotlibDeprecationWarning:
Passing one of 'on', 'true', 'off', 'false' as a boolean is deprecated; use an actual boolean (True/False) instead.
warn_deprecated("2.2", "Passing one of 'on', 'true', 'off', 'false' as a "
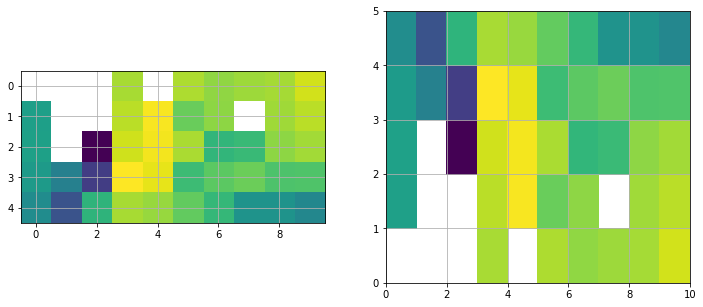
f, ax = plt.subplots(1, 1, figsize=(12, 5))
c = ax.pcolormesh(lon, lat, T1850)
plt.colorbar(c)
<matplotlib.colorbar.Colorbar at 0x115b63c88>
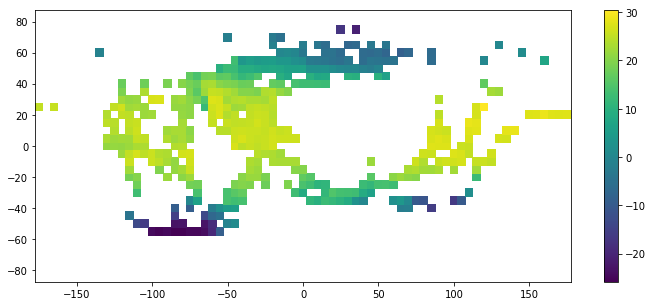
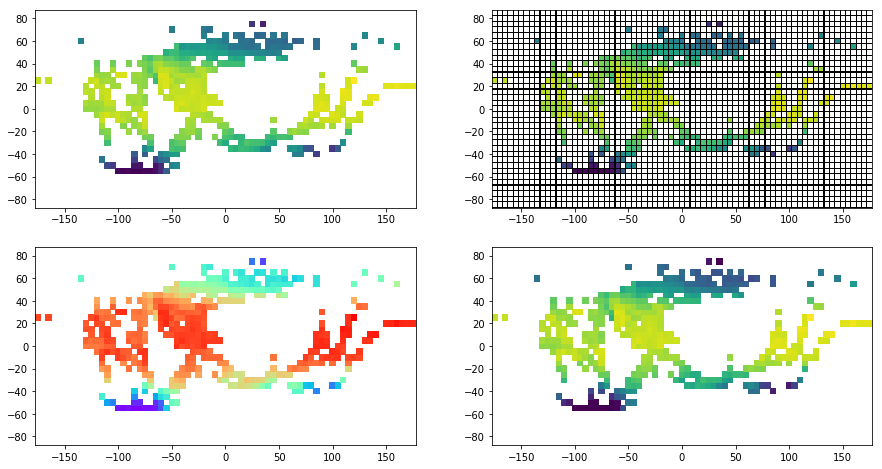
f, ax = plt.subplots(2, 2, figsize=(15, 8))
# pcolor() can be very slow for large arrays.
# In most cases you should use the similar but much faster pcolormesh instead
ax[0,0].pcolor(lon, lat, T1850)
ax[0,1].pcolormesh(lon, lat, T1850, edgecolors='black', linewidth=.1)
ax[1,0].pcolormesh(lon, lat, T1850, cmap='rainbow') # more at https://matplotlib.org/examples/color/colormaps_reference.html
ax[1,1].pcolormesh(lon, lat, T1850, vmin=-20, vmax=30)
<matplotlib.collections.QuadMesh at 0x115841ac8>
contour / contourf
contour and contourf draw contour lines and filled contours, respectively.
You can pass the grid information to these functions.
T2018 = T[0, :, :] + Tanom[2016, :, :] # monthly mean T for 2018 January
f, ax = plt.subplots(1, 2, figsize=(16, 5))
c0 = ax[0].contour(lon, lat, T2018)
plt.colorbar(c0, ax=ax[0])
c1 = ax[1].contourf(lon, lat, T2018)
plt.colorbar(c1, ax=ax[1])
<matplotlib.colorbar.Colorbar at 0x115e1b438>

You can decide how many contours to show in two different ways: a number of contours or an actual range
f, ax = plt.subplots(1, 2, figsize=(16, 5))
c0 = ax[0].contour(lon, lat, T2018, 20)
ax[0].clabel(c0, inline=1, fontsize=10, fmt='%2.1f')
c1 = ax[1].contourf(lon, lat, T2018, np.arange(0, 21, 5), extend='both')
# ax[1].clabel(c1)
plt.colorbar(c1, ax=ax[1])
<matplotlib.colorbar.Colorbar at 0x119b52ac8>

Quiver
This is useful when you want to show the wind or ocean current.
Let’s read the wind data.
f = Dataset('uwnd.mon.mean.nc', 'r')
print(f.variables.keys())
uwind = f.variables['uwnd'][:] # monthly data
lon = f.variables['lon'][:]
lat = f.variables['lat'][:]
f.close()
f = Dataset('vwnd.mon.mean.nc', 'r')
print(f.variables.keys())
vwind = f.variables['vwnd'][:] # monthly data
lon = f.variables['lon'][:]
lat = f.variables['lat'][:]
f.close()
odict_keys(['lat', 'lon', 'time', 'uwnd'])
odict_keys(['lat', 'lon', 'time', 'vwnd'])
help(plt.quiver)
Help on function quiver in module matplotlib.pyplot:
quiver(*args, data=None, **kw)
Plot a 2-D field of arrows.
Call signatures::
quiver(U, V, **kw)
quiver(U, V, C, **kw)
quiver(X, Y, U, V, **kw)
quiver(X, Y, U, V, C, **kw)
*U* and *V* are the arrow data, *X* and *Y* set the location of the
arrows, and *C* sets the color of the arrows. These arguments may be 1-D or
2-D arrays or sequences.
If *X* and *Y* are absent, they will be generated as a uniform grid.
If *U* and *V* are 2-D arrays and *X* and *Y* are 1-D, and if ``len(X)`` and
``len(Y)`` match the column and row dimensions of *U*, then *X* and *Y* will be
expanded with :func:`numpy.meshgrid`.
The default settings auto-scales the length of the arrows to a reasonable size.
To change this behavior see the *scale* and *scale_units* kwargs.
The defaults give a slightly swept-back arrow; to make the head a
triangle, make *headaxislength* the same as *headlength*. To make the
arrow more pointed, reduce *headwidth* or increase *headlength* and
*headaxislength*. To make the head smaller relative to the shaft,
scale down all the head parameters. You will probably do best to leave
minshaft alone.
*linewidths* and *edgecolors* can be used to customize the arrow
outlines.
Parameters
----------
X : 1D or 2D array, sequence, optional
The x coordinates of the arrow locations
Y : 1D or 2D array, sequence, optional
The y coordinates of the arrow locations
U : 1D or 2D array or masked array, sequence
The x components of the arrow vectors
V : 1D or 2D array or masked array, sequence
The y components of the arrow vectors
C : 1D or 2D array, sequence, optional
The arrow colors
units : [ 'width' | 'height' | 'dots' | 'inches' | 'x' | 'y' | 'xy' ]
The arrow dimensions (except for *length*) are measured in multiples of
this unit.
'width' or 'height': the width or height of the axis
'dots' or 'inches': pixels or inches, based on the figure dpi
'x', 'y', or 'xy': respectively *X*, *Y*, or :math:`\sqrt{X^2 + Y^2}`
in data units
The arrows scale differently depending on the units. For
'x' or 'y', the arrows get larger as one zooms in; for other
units, the arrow size is independent of the zoom state. For
'width or 'height', the arrow size increases with the width and
height of the axes, respectively, when the window is resized;
for 'dots' or 'inches', resizing does not change the arrows.
angles : [ 'uv' | 'xy' ], array, optional
Method for determining the angle of the arrows. Default is 'uv'.
'uv': the arrow axis aspect ratio is 1 so that
if *U*==*V* the orientation of the arrow on the plot is 45 degrees
counter-clockwise from the horizontal axis (positive to the right).
'xy': arrows point from (x,y) to (x+u, y+v).
Use this for plotting a gradient field, for example.
Alternatively, arbitrary angles may be specified as an array
of values in degrees, counter-clockwise from the horizontal axis.
Note: inverting a data axis will correspondingly invert the
arrows only with ``angles='xy'``.
scale : None, float, optional
Number of data units per arrow length unit, e.g., m/s per plot width; a
smaller scale parameter makes the arrow longer. Default is *None*.
If *None*, a simple autoscaling algorithm is used, based on the average
vector length and the number of vectors. The arrow length unit is given by
the *scale_units* parameter
scale_units : [ 'width' | 'height' | 'dots' | 'inches' | 'x' | 'y' | 'xy' ], None, optional
If the *scale* kwarg is *None*, the arrow length unit. Default is *None*.
e.g. *scale_units* is 'inches', *scale* is 2.0, and
``(u,v) = (1,0)``, then the vector will be 0.5 inches long.
If *scale_units* is 'width'/'height', then the vector will be half the
width/height of the axes.
If *scale_units* is 'x' then the vector will be 0.5 x-axis
units. To plot vectors in the x-y plane, with u and v having
the same units as x and y, use
``angles='xy', scale_units='xy', scale=1``.
width : scalar, optional
Shaft width in arrow units; default depends on choice of units,
above, and number of vectors; a typical starting value is about
0.005 times the width of the plot.
headwidth : scalar, optional
Head width as multiple of shaft width, default is 3
headlength : scalar, optional
Head length as multiple of shaft width, default is 5
headaxislength : scalar, optional
Head length at shaft intersection, default is 4.5
minshaft : scalar, optional
Length below which arrow scales, in units of head length. Do not
set this to less than 1, or small arrows will look terrible!
Default is 1
minlength : scalar, optional
Minimum length as a multiple of shaft width; if an arrow length
is less than this, plot a dot (hexagon) of this diameter instead.
Default is 1.
pivot : [ 'tail' | 'mid' | 'middle' | 'tip' ], optional
The part of the arrow that is at the grid point; the arrow rotates
about this point, hence the name *pivot*.
color : [ color | color sequence ], optional
This is a synonym for the
:class:`~matplotlib.collections.PolyCollection` facecolor kwarg.
If *C* has been set, *color* has no effect.
Notes
-----
Additional :class:`~matplotlib.collections.PolyCollection`
keyword arguments:
agg_filter: a filter function, which takes a (m, n, 3) float array and a dpi value, and returns a (m, n, 3) array
alpha: float or None
animated: bool
antialiased: bool or sequence of bools
array: ndarray
capstyle: {'butt', 'round', 'projecting'}
clim: a length 2 sequence of floats; may be overridden in methods that have ``vmin`` and ``vmax`` kwargs.
clip_box: `.Bbox`
clip_on: bool
clip_path: [(`~matplotlib.path.Path`, `.Transform`) | `.Patch` | None]
cmap: colormap or registered colormap name
color: matplotlib color arg or sequence of rgba tuples
contains: callable
edgecolor: color or sequence of colors
facecolor: color or sequence of colors
figure: `.Figure`
gid: str
hatch: {'/', '\\', '|', '-', '+', 'x', 'o', 'O', '.', '*'}
in_layout: bool
joinstyle: {'miter', 'round', 'bevel'}
label: object
linestyle: {'-', '--', '-.', ':', '', (offset, on-off-seq), ...}
linewidth: float or sequence of floats
norm: `.Normalize`
offset_position: {'screen', 'data'}
offsets: float or sequence of floats
path_effects: `.AbstractPathEffect`
picker: None or bool or float or callable
pickradius: unknown
rasterized: bool or None
sketch_params: (scale: float, length: float, randomness: float)
snap: bool or None
transform: `.Transform`
url: str
urls: List[str] or None
visible: bool
zorder: float
See Also
--------
quiverkey : Add a key to a quiver plot
f, ax = plt.subplots(1, 1, figsize=(16, 8))
q = ax.quiver(lon, lat, uwind[-1, :, :], vwind[-1, :, :])
# q = ax.quiver(lon, lat, uwind[-1,...], vwind[-1,...])

Although we have the plot with arrows, it is not easy to see their sizes and direction.
It seems that there needs some tunings.
help(plt.quiverkey)
Help on function quiverkey in module matplotlib.pyplot:
quiverkey(Q, X, Y, U, label, **kw)
Add a key to a quiver plot.
Call signature::
quiverkey(Q, X, Y, U, label, **kw)
Arguments:
*Q*:
The Quiver instance returned by a call to quiver.
*X*, *Y*:
The location of the key; additional explanation follows.
*U*:
The length of the key
*label*:
A string with the length and units of the key
Keyword arguments:
*angle* = 0
The angle of the key arrow. Measured in degrees anti-clockwise from the
x-axis.
*coordinates* = [ 'axes' | 'figure' | 'data' | 'inches' ]
Coordinate system and units for *X*, *Y*: 'axes' and 'figure' are
normalized coordinate systems with 0,0 in the lower left and 1,1
in the upper right; 'data' are the axes data coordinates (used for
the locations of the vectors in the quiver plot itself); 'inches'
is position in the figure in inches, with 0,0 at the lower left
corner.
*color*:
overrides face and edge colors from *Q*.
*labelpos* = [ 'N' | 'S' | 'E' | 'W' ]
Position the label above, below, to the right, to the left of the
arrow, respectively.
*labelsep*:
Distance in inches between the arrow and the label. Default is
0.1
*labelcolor*:
defaults to default :class:`~matplotlib.text.Text` color.
*fontproperties*:
A dictionary with keyword arguments accepted by the
:class:`~matplotlib.font_manager.FontProperties` initializer:
*family*, *style*, *variant*, *size*, *weight*
Any additional keyword arguments are used to override vector
properties taken from *Q*.
The positioning of the key depends on *X*, *Y*, *coordinates*, and
*labelpos*. If *labelpos* is 'N' or 'S', *X*, *Y* give the position
of the middle of the key arrow. If *labelpos* is 'E', *X*, *Y*
positions the head, and if *labelpos* is 'W', *X*, *Y* positions the
tail; in either of these two cases, *X*, *Y* is somewhere in the
middle of the arrow+label key object.
f, ax = plt.subplots(1, 1, figsize=(16, 8))
# Try to show arrows at every three points.
intv = 3
q = ax.quiver(lon[::intv], lat[::intv], uwind[-1, ::intv, ::intv], vwind[-1, ::intv, ::intv])
qk = ax.quiverkey(q, 10, 95, 10, '10 m/s', labelpos='E', coordinates='data',
color='r', labelcolor='r', fontproperties={'size': 15})

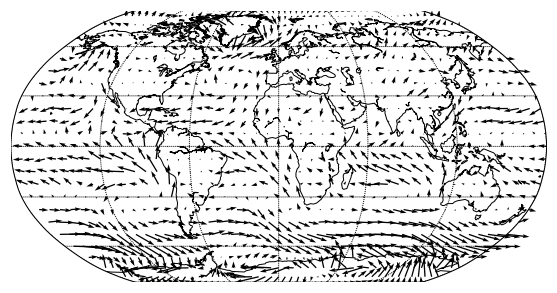
from mpl_toolkits.basemap import Basemap
X, Y =np.meshgrid(lon, lat)
plt.figure(figsize=(15,5))
m = Basemap(projection='robin',lon_0=0,resolution='c')
m.drawcoastlines()
m.drawparallels(np.arange(-90.,120.,30.))
m.drawmeridians(np.arange(0.,360.,60.))
m.quiver(X[::intv, ::intv], Y[::intv, ::intv], uwind[-1, ::intv, ::intv], vwind[-1, ::intv, ::intv], latlon=True)